La suite de Fibonacci est définie par :
u0 = 0
u1 = 1
un+1 = un+un-1
Le nombre d’or est défini par :
un+1/un pour n tendant vers l’infini.
Ce qui donne :
2,2.000000
3,1.500000
5,1.666667
8,1.600000
13,1.625000
21,1.615385
34,1.619048
55,1.617647
89,1.618182
144,1.617978
233,1.618056
377,1.618026
610,1.618037
987,1.618033
1597,1.618034
Le nombre d’or est égale à : (1+sqrt(5))/2
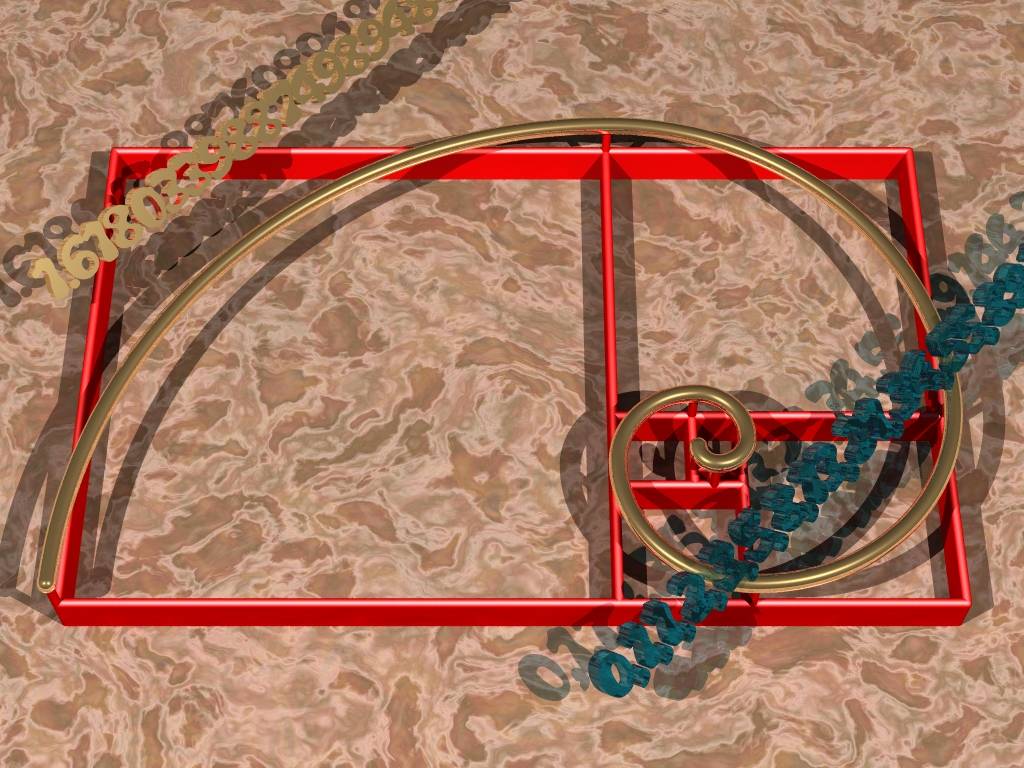
Illustré graphiquement ça donne un rectangle qu’on peut subdiviser à l’infini et qui donne un rectangle de même proportions. Et en déroulant un spirale dans ce rectangle on obtient la spirale d’or.